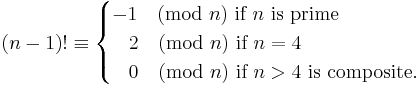Composite number

A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number.

So, if n > 0 is an integer and there are integers 1 < a, b < n such that n = a × b, then n is composite. By definition, every integer greater than one is either a prime number or a composite number. The number one is a unit – it is neither prime nor composite. For example, the integer 14 is a composite number because it can be factored as 2 × 7. Likewise, the integers 2 and 3 are not composite numbers because each of them can only be divided by one and itself.

The first 105 composite numbers (sequence A002808 in OEIS) are

4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 105, 106, 108, 110, 111, 112, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 128, 129, 130, 132, 133, 134, 135, 136, 138, 140.

Every composite number can be written as the product of two or more (not necessarily distinct) primes; furthermore, this representation is unique up to the order of the factors. This is called the fundamental theorem of arithmetic.

Wilson's theorem provides a test for whether a number is prime or composite:

(n-1)! \equiv \begin{cases} -1 \pmod{n} \mbox{ if } n \mbox{ is prime}\\ \;\;\; 2 \pmod{n} \mbox{ if } n =4\\ \;\;\;0 \pmod{n} \mbox{ if } n >4 \mbox{ is composite}. \end{cases}

Types of composite numbers

One way to classify composite numbers is by counting the number of prime factors. A composite number with two prime factors is a semiprime or 2-almost prime (the factors need not be distinct, hence squares of primes are included). A composite number with three distinct prime factors is a sphenic number. In some applications, it is necessary to differentiate between composite numbers with an odd number of distinct prime factors and those with an even number of distinct prime factors. For the latter

\mu(n) = (-1)^{2x} = 1\,

(where μ is the Möbius function and x is half the total of prime factors), while for the former

\mu(n) = (-1)^{2x %2B 1} = -1.\,

Note however that for prime numbers the function also returns -1, and that 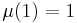\mu(1) = 1. For a number n with one or more repeated prime factors, \mu(n) = 0.

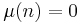If all the prime factors of a number are repeated it is called a powerful number. If none of its prime factors are repeated, it is called squarefree. (All prime numbers and 1 are squarefree.)

Another way to classify composite numbers is by counting the number of divisors. All composite numbers have at least three divisors. In the case of squares of primes, those divisors are 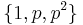\{1, p, p^2\}. A number n that has more divisors than any x < n is a highly composite number (though the first two such numbers are 1 and 2).

See also

External links